cbasspy.mapManipulations package¶

Submodules¶

cbasspy.mapManipulations.beam2bl module¶

PnX(l, x)¶

beam2bl_I(beam, theta, lmax, xtheta=True, calc_err=False)¶

Calculates the Legendre Transform of an I beam. Uses the integrator in cbasspy.mapManipulations.integrate and the recurisve relationships between Legendre polynomials.

Parameters:

beam : array_like

Array of beam values.

theta : array_like

Corresponding array of theta values.

lmax : int

Maximum l you want to calculate the Legendre Transform to.

xtheta : optional {True,False}

Set to True if you want to use theta as the x variable, False to use cos(theta).

calc_err : optional, {True,False}

Set to True if you want to calculate an estimate of the truncation error. Note this has not been well tested, in particular the calculation of the 6th order derivative of the integrand!

Returns:

ell : array_like

0 to lmax.

window : array_like

The window function at each ell.

err : float, optional

Truncation error estimate.

See also

beam2bl_P: Equivalent function but for polarization window functions.

beam2bl_P(beam, theta, lmax, xtheta=True, calc_err=False)¶

Function for calculating the spin-2 Legendre Transform of the beam. Uses the integrator in cbasspy.mapManipulations.integrate, and the recurisve relationships between Legendre polynomials and their derivatives.

Parameters:

beam : array_like

Array of beam values.

theta : array_like

Corresponding array of theta values.

lmax : int

Maximum l you want to calculate the Legendre Transform to.

xtheta : optional, {True,False}

Set to True is you want to use theta as the x variable, set to False to use cos(theta).

calc_err : optional, {True,False}

Set to True if you want to return an estimate of the truncation error. Note this has note been tested well, particularly the calculation of the 6th derivative of the integrand!

Returns:

ell : array_like

0 to lmax

window : array_like

The spin-2 window function at each ell

err : float, optional

Estimate of the truncation error (optional)

See also

beam2bl_I: Equivalent function but for total intensity window functions.

cbasspy.mapManipulations.beam2bl_I module¶

beam2bl_I(beam, theta, lmax, xtheta=True)¶

Calculates the Legendre Transform of an I beam. Uses the integrator in integrate.py and the recurisve relationships between Legendre polynomials.

Required arguments: beam - Array of beam values. theta - Corresponding array of theta values. lmax - Maximum l you want to calculate the Legendre Transform to.

Optional arguments: xtheta - True/False. Set to True if you want to use theta as the x variable,

False to use cos(theta).

calc_err - True/False. Set to True if you want to calculate an estimate of the truncation error.: Note this has not been well tested, in particular the calculation of the 6th order derivative of the integrand!

Returns: ell - 0:lmax window - the window function at each ell err - truncation error estimate (optional)

History: 15/02/2018 - RG Created 16/02/2018 - LJ Removed plotting 26/02/2018 - RG Added truncation error estimates

cbasspy.mapManipulations.beam2bl_P module¶

beam2bl_P(beam, theta, lmax, xtheta=True, calc_err=False)¶

Function for calculating the spin-2 Legendre Transform of the beam. Uses the integrator in integrate.py, and the recurisve relationships between Legendre polynomials and their derivatives.

Required arguments are:

beam - Array of beam values.
theta - Corresponding array of theta values.
lmax - Maximum l you want to calculate the Legendre Transform to.

Optional arguments:

xtheta - True/False. Set to True if you want to use theta as the x variable, False to use cos(theta).
calc_err - True/False. Set to True if you want to return an estimate of the truncation error. Note this has note been tested well, particularly the calculation of the 6th derivative of the integrand!

Returns:

ell - 0:lmax window - The spin-2 window function at each ell err - Estimate of the truncation error (optional)

cbasspy.mapManipulations.deconvolveMap module¶

createN2S(inMap, ell, doPol=True, ellMin=10.0, ellMax=100.0, spice_name='spice_TEB_spectra.txt', temp_signal_name='_temporaryDeconv_IQU_signal.fits')¶

Function to estimate the noise-to-signal ratio as a function of ell. The noise level is determined from the 10th from last element in the signal spectrum. The signal level is determined from a straight line fit to log(Cl)/log(ell) in the range [ellMin:ellMaxx]. The noise-to-signal ratio is retured at ell

Parameters:

inMap : array_like

Input healpix sky map

ell : array_like

Multipole moments to return the N2S ratio at

doPol : bool, True

Whether to do T or TEB

ellMin : float, 10.

Lower bound of ell range to fit signal straight line to

ellMax : float, 100.

Upper bound of ell range to fit signal straight line to

spice_name : str, ‘spice_TEB_spectra.txt’

Name of spice parameter file to use, it looks in the cbasspy/mapManipulations directory.

temp_signal_name : str, ‘_temporaryDeconv_IQU_signal.fits’

What to save a temporary map as in the current working directory.

Returns:

N2S : array_like

Array of noise-to-signal ratios. Either TT or [TT,EE,BB]

createWindowsFromRimo(rimo_file_name, fwhm, windowFileName, ext_name='BEAMWF_030X030', saveWindowFns=True, extend_ell=False, extend_ell_max=2048)¶

Load the beam Bls from a Planck RIMO file and create the window functions required to

deconvolve to a Gaussian beam. If the output is saved to a file then it can be loaded in by deconvolveMap()

Parameters:

rimo_file_name : str

Name of Planck RIMO fits file

fwhm : float

Gaussian beam to smooth to [radians]

windowFileName : str

Name of file to save window functions to. The saved files have the format [windowFileName]I.txt and [windowFileName]P.txt

ext_name : str, ‘BEAMWF_030X030’

Name of fits extension containing beam Bls

saveWindowFns : optional {True, False}

Whether to save the window functions so that they can be loaded in the future

Returns:

ell : array_like

Multipole moments

inBeamBl_I : array_like

Input Planck beam

inBeamBl_P : array_like

Input Planck beam, note this is the same as inBeamBl_I

outBeamBl_I : array_like

Gaussian beam to smooth to

outBeamBl_P : array_like

Gaussian beam to smooth to

ratio_I : array_like

alm reweighting function

ratio_P : array_like

alm reweighting function

createWindowsFromTxt(txt_file_name, fwhm, windowFileName, saveWindowFns=True, extend_ell=False, extend_ell_max=2048)¶

Load the beam Bls from a WMAP txt file and create the window functions required to deconvolve to a Gaussian beam. If the output is saved to a file then it can be loaded in by deconvolveMap()

Parameters:

txt_file_name : str

Name of WMAP txt file

fwhm : float

Gaussian beam to smooth to [radians]

windowFileName : str

Name of file to save window functions to. The saved files have the format [windowFileName]I.txt and [windowFileName]P.txt

ext_name : str, ‘BEAMWF_030X030’

Name of fits extension containing beam Bls

saveWindowFns : optional {True, False}

Whether to save the window functions so that they can be loaded in the future

Returns:

ell : array_like

Multipole moments

inBeamBl_I : array_like

Input Planck beam

inBeamBl_P : array_like

Input Planck beam, note this is the same as inBeamBl_I

outBeamBl_I : array_like

Gaussian beam to smooth to

outBeamBl_P : array_like

Gaussian beam to smooth to

ratio_I : array_like

alm reweighting function

ratio_P : array_like

alm reweighting function

deconvolveMap(inMap, theta, beam, fwhm, NSIDE_out, niter=3, inCov=None, returnLots=False, saveWindowFns=False, loadWindowFns=False, windowFileName='windowFunctions', inMapCoord='c', useDecMask=False, outMapCoord='g', cutMin=-90, cutMax=0, numOfNoiseSims=3, doTapering=False, ell_min=200, ell_max=2000, doWiener=False, dgUsingAlms=False)¶

Function to deconvolve a map, smooth to fwhm and downgrade to NSIDE_out.

Parameters:

inMap : array_like

Input map to be smoothed, in Ta (antenna temperature). Shape (npix,) or (n,npix)

theta : array_like

Array of angles at which the beam is sampled in radians

beam : array_like

Beam profile at each angle

fwhm : float

Gaussian beam to smooth to [radians]

NSIDE_out : int

Nside to downgrade output map to

niter : int, optional {3}

Number of iterations when estimating alms from map

inCov : array_like, optional {None]

Covariance map, if None then not used. Should take one of three forms [cov(I)] or [cov(I),cov(Q),cov(U)] or [cov(I),cov(Q),cov(U),cov(IQ),cov(IU),cov(QU)] and have shape (npix,), or (3,npix) or (6,npix). Note that the covariances are not used, only the variances.

returnLots : optional, {False,True}

If False, only returns smoothed map If True, also returns ell, inBeamBl, outBeamBl, ratio, omega_beam and omega_out

saveWindowFns : optional {True,False}

Whether to save the window functions so that they can be loaded in the future

loadWindowFns : optional {True,False}

whether to load in window functions from txt file. NOTE, this overrides theta, beam and fwhm given earlier

windowFileName : str, optional, {‘windowFunctions’}

Name of file to save window functions to or to load them from The saved files have the format [windowFileName]I.txt and [windowFileName]P.txt

useDecMask : optional, {True,False}

Whether to apply a declination mask the the smoothed and downgraded map

inMapCoord : str, optional {‘C’,’G’,’E’}

The coordinate system of the input map.

outMapCoord : str, optional {‘C’,’G’,’E’}

The coordinate system to rotate the map to.

cutMin : float, optional {-90}

The minimum declination to cut in degrees.

cutMax : float, optional {0}

The maximum declination to cut in degrees.

numOfNoiseSims : int, optional {3}

The scaling factors for the smoothed variance maps are estimated from simulated realisations of the noise. This integer determines how many simulations to use.

doTapering : optional {False,True}

Whether to apply a cosine taper to the window function.

ell_min : int, optional {200}

When to begin the tapering.

ell_max : int, optional {2000}

When to finish tapering.

doWiener : bool, False

Whether to do wiener deconvolution. See createN2S() and the How To doc. for details.

dgUsingAlms : bool, False

If True, downgrade Nside on E and B maps, not Q and U maps. No effect if just I map.

Returns:

outMap : array_like

Smoothed and downgraded maps. Has shape (npix_out,) or (3,npix_out)

outVarMap : array_like

Smoothed and downgraded variance maps. Has same shape as outMap.

If inCov was None, then this is also None.

outVarMapScaleFactor : float

This should be appllied to outVarMap to correct for smoothing and downgrading. Has shape (1) or (3).

ell : array_like, optional

Multipole moments of the window functions.

inBeamBl_I : array_like, optional

I beam window function

inBeamBl_P : array_like, optional

P beam window function

outBeamBl_I : array_like, optional

I outbeam window fuction

outBeamBl_P : array_like, optional

P outbeam window function

ratio_I : array_like, optional

alm reweighting function in I. If doWiener==True then this includes the Wiener weighting.

ratio_P : array_like, optional

alm reweighting function in P. Note, if doing a Wiener deconvolution then E and B have different N2S ratios and are treated separately.

omega_beam : float, optional

in beam solid angle [radians]

omega_out : float, optional

outbeam solid angle [radians]

ratio_E : array_like, optional

Only returned if (returnLots==True)&(doWiener==True) The reweighting function accounting for Wiener filtering

ratio_B : array_like, optional

Only returned if (returnLots==True)&(doWiener==True) The reweighting function accounting for Wiener filtering

N2S : array_like, optional

Only returned if (returnLots==True)&(doWiener==True) The noise-to-signal estimates for TT (and EE and BB if polarization is turned on)

interp_kink(window_file, lmin, lmax, no_ell, pol, save_window=False, window_out_dir='.', create_plot=False, plot_out_dir='.')¶

Function for removing the kink in the C-BASS window function, replacing it with a smooth interpolated function between lmin and lmax.

Returns:

ell: The input ells. numpy.ndarray

new_bl: The new beam bl’s, with the smoothed kink. numpy.ndarray

gl: The input Gaussian window. numpy.ndarray

new_rl: The new window function ratio, with the smoothed kink. numpy.ndarray

rotateMap(inMap, inCov, incoord, outcoord)¶

Wrapper to rotate map and variance map.

Parameters:

inMap : array_like

Input map, can have shape [npix,3], [npix,]. If shape [npix,3] then assumes [Imap,Qmap,Umap]

inCov : array_like

Input covariance map. Can have shape [npix,3], [npix,]

incoord : str, {‘E’,’C’,’G’}

Coordinate system of input map

outcoord : str, {‘E’,’C’,’G’}

Coordinate system of output map

Returns:

outMap : array_like

Rotated map

outCov : array_like

Rotated covariance map

smoothVarMap(inVar, ratio, dgUsingAlms=False, dgAlmNside=64)¶

Reweights the variance map in alm space with ratio and does the same to a realisation of the noise.

Parameters:

inVar : array_like

Variance maps either var(I) with shape (npix,) or [var(I),var(Q),var(U)] with shape (3,npix). e.g., inVar = np.array([inCov[0],inCov[1],inCov[2]])

ratio : array_like

alm reweighting functions, with shape (lmax+1,) if just I or (3,lmax+1) if I,Q and U. e.g., ratio = np.array([ratio_I,ratio_P,ratio_P])

dgUsingAlms : book, False

If True, downgrade during alm2map else don’t downgrade

dgAlmNside : int, 64

The Nside to downgrade to

Returns:

outVarMap : array_like

smoothed var map with same shape as inVar

outNoiseMap : array_like

smoothed noise realisation map with same shape as inVar

taperFn(ell, ell_min, ell_max)¶

Calculate a cosine taper function.

Parameters:

ell : array_like

ell values at which to evalutate the taper.

ell_min : int

where the cosine taper starts.

ell_max : int

where the cosine taper ends.

Returns:

taper : array_like

Taper function evaluated at l values in ell.

cbasspy.mapManipulations.integrate module¶

This module is used to numerically integrate tabulated data using the Newton-Cotes method of arbitrary order.

i.e. it is an approximation to 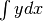$\int y dx$ .

Although these functions live in cbasspy.mapManipulations they will likely find use outside of this context!

integrateData(x, y, order, return_err=False)¶

Integrates y over the x range, splitting the data up into intervals of length order and using the Newton-Cotes method on the intervals.

Parameters:

x : array_like

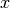$x$ -ordinates.

y : array_like

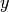$y$ -absicia

order : int

Maximum length of data to integrate in one go.

return_err : optional, {True,False}

Return the average error coefficient if True.

Returns:

integral : float

Integral of y over the x range.

error : float

Average error coefficient. (optional)

See also

integrateInterval: The Newton-Cotes integration function.

integrateInterval(x_sub, y_sub)¶

Integrates y_sub over the range of x_sub, using the newton_cotes method. Will fail if length of data is too long.

This is called by cbasspy.mapManipulations.integrateData(). Usually you will want to call the integrate function, rather than this one.

Parameters:

x_sub : array_like

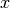$x$ -ordinates

y_sub: array_like

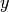$y$ -absicia

Returns:

integral : float

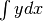$\int y dx$ over the range of $x$ .

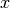error : float

Newton-Cotes error coefficient.

See also

integrateData: A function that calls this in a sensible way.

cbasspy.mapManipulations.pix_QU_rot module¶

pix_rotate_QU(vec1, vec2, Q, U)¶

This code calculates the rotation in the local coordinate axes defining Q and U at the position defined by the vector vec1, when rotating to the position given by the vector vec2. The subsequent transformation in Q and U is then calculated.

This can be compared to the global QU rotation code, where we consider the change in Q and U across the whole sky under the action of some global coordinate change.

Parameters:

vec1 : array_like, [3,]

Position of the original pixel centre, described by unit vector vec1.

vec2 : array_like, [3,]

Position of the final pixel centre, decribed by unit vector vec2.

Q : float

The Q value in the pixel specified by vec1.

U : float

The U value in the pixel specified by vec2.

Returns:

Qprime : float

The Q value in the parent pixel, specified by vec2.

Uprime : float

The U value in the parent pixel, specified by vec2.

Notes

The angle-axis rotation matrix between vec1 and vec2 is given by:

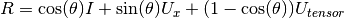
$R = \cos(\theta)I + \sin(\theta)U_x + (1 - \cos(\theta))U_{tensor}$

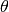$\theta$ - angle of rotation about the Euler axis.
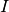$I$ - Identity matrix.
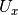$U_x$ - Cross matrix of vector u, the unit vector defining the Euler axis/
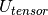$U_{tensor}$ - Tensor product of the vector u.

There are an infinite number of rotation matrices that can map from one vector to another, we have just chosen a convenient form.

cbasspy.mapManipulations.rotate_QU module¶

Module for rotating I, Q and U maps in pixel space.

rotate_ang_QU(Qmap, Umap, alpha, beta, gamma)¶

This code rotates the Q and U maps, given a set of Euler angles defining the rotation.

Parameters:

Qmap : array_like

The input HEALPix Q map, in the input coordinate system.

Umap : array_like

The input HEALPix U map, in the input coordinate system.

alpha : float

The first Euler angle, in degrees (rotation counterclockwise around original Z).

beta : float

The second Euler angle, in degrees (rotation counterclockwise around interim Y).

gamma : float

The third Euler angle, in degrees (rotation counterclockwise around final X).

Returns:

Qrot_map : array_like

Rotated Q map

Urot_map : array_like

Rotated U map

See also

rotate_coord_QU: Rotate Q and U maps between different coordinate systems.

rotate_coord_I(inmap, incoord, outcoord, interpEdgeValue=-5.0)¶

Script to rotate an I map in pixel space Performs rotation by interpolating onto new map.

Parameters:

inmap : array_like [npix,]

Total intensity HEALPix map

incoord : str {‘e’,’c’,’g’}

Coordinate system of input map

outcoord : str {‘e’,’c’,’g’}

Coordinate system of output map

interpEdgeValue : float, {-5.0}

The interpolation can cause strange results near the edge of the map. Anything smaller than this value after rotation will be set to the UNSEEN value.

Returns:

rotatedMap : array_like

HEALPix map rotated to new coordinate system.

See also

rotate_coord_QU: Rotate Q and U maps between different coordinate systems.

rotate_coord_QU(Qmap, Umap, incoord, outcoord, isVarMap=False)¶

This code calculates the rotation of Q and U, at the position of some vector in input coordinates, under the rotation from the input to output coordinates (i.e. what happens to the orientation of the local coordinate axes defining Q and U when we change from the input to output coordinates, and apply the corresponding rotation to Q and U).

Parameters:

Qmap : array_like

Input HEALPix Q map, in the input coordinate system.

Umap : array_like

Input Healpix U map, in the input coordinate system.

incoord : str, {‘E’,’C’,’G’}

The input coordinate system.

outcoord : str, {‘E’,’C’,’G’}

The output coordinate system.

isVarMap : optional, {False,True}

Are the input Q and U maps variance maps?

Returns:

Qrot_map : array_like

Rotated Q map.

Urot_map : array_like

Rotated U map.

See also

rotate_coord_I: Rotate I map between coordinate systems.
rotate_ang_QU: Rotate Q and U maps using Euler angles.

cbasspy.mapManipulations package¶

Submodules¶

cbasspy.mapManipulations.beam2bl module¶

cbasspy.mapManipulations.beam2bl_I module¶

cbasspy.mapManipulations.beam2bl_P module¶

cbasspy.mapManipulations.deconvolveMap module¶

cbasspy.mapManipulations.integrate module¶

cbasspy.mapManipulations.pix_QU_rot module¶

cbasspy.mapManipulations.rotate_QU module¶

cbasspy.mapManipulations.wl_anafast module¶

Table Of Contents

Related Topics

This Page