We mentioned during the 'Beam me up' simulation that the primary beam pattern scales with frequency, and it is this property that we are going to investigate with this simulation.

We will start once again with the KAT-7 array, however we're going to take out the 12 metre dishes, and give it 25 metre VLA dishes instead. Also, instead of a simplistic analytic formula for the primary beam, we're going to use simulated beam patterns read in as FITS files. MeqTrees has the capability of reading in such files and performing interpolation, as well as adding rotation effects that simulate the rotation of the beam pattern on the sky due to the azimuth-elevation mounts of the VLA antennas.

The beam patterns themselves are a bit closer to reality than what can be achieved with a simple analytic approximation for the VLA beam. (Note that the cos-cubed function used previously does a very good job of representing the main lobe of the WSRT beam, however the WSRT is famed for its stable beam, thanks in part to its equatorial mount system.) The beam FITS images we'll use here are generated by Walter Brisken's Cassbeam software which uses ray tracing to compute the beam patterns of Cassegrain dishes. It performs the calculation in full polarization, and the end result is a complex-valued 2x2 Jones matrix describing the response pattern of the dish to incoming radiation.

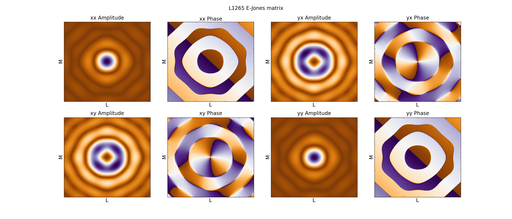
A visualisation of such a beam pattern (in this case at 1.265 GHz) is attached below (the colour scale maxes out with purple). A complex valued (in this case amplitude and phase) 2x2 matrix thus results in eight FITS images to full describe the beam. As you can see there is some complex structure away from the main lobe that is not azimuthally symmetric. This arises as radiation scatters off the support struts that hold the secondary reflector for the Cassegrain optics. The VLA antennas have four of these support legs giving rise to the 4-fold symmetry of the first sidelobe.

We're also going to give our observation a bandwidth of 1 - 2 GHz (also the same as the VLA L-band bandwidth). This gives a fractional bandwidth, defined here as the ratio of the bandwidth to the centre frequency, of about 67%. The higher this percentage is, the more significant you can expect the frequency-related effects across the band to be.

For this simulation we select six frequencies across the band: 1.0, 1.2, 1.4, 1.6, 1.8 and 2.0 GHz. Attached below are six KAT-7 Measurement Sets at these frequencies, each with a single 50 MHz channel, and again using a 12 hour track.

To see the effects of the beam we also need six beam patterns at the relevant frequencies. We'll take a bit of an ideal-world shortcut here to make the problem leaner, and discard the beam patterns that include the cross-hands of polarization (XY and YX). This is how you would ideally like your instrument to behave: your instrumental Jones matrices all having unity gain on the XX,YY (or LL,RR; or HH,VV) diagonals (or at least the sort of decent behaviour that can be replicated with a little bit of linear algebra), and zeros on the XY,YX (or LR, RL; or HV; VH) off diagonals, that is to say the instrument does not interfere with your polarization measurements at all. In reality the E-Jones matrix of your antenna will stamp its authority on your the polarization state of the incoming radiation.

The pair of feeds that are sensitive to the two orthogonal polarization states are separate entities and thus can't be co-spatial, and this always results in some sort of instrumental polarization, manifested by the patterns in the XY and YX plots below. The more eagle-eyed reader might be able to discern a slight offset between the amplitude peaks of the XX and YY images in the image below. Find a VLA person and ask him or her about beam squint.

(The same VLA person will probably also point out that we're using linear X/Y feeds when in reality the VLA has circular L/R feeds, but don't worry, it's a simulation and we're omnipotent. You can always point out that the VLA doesn't consist of seven antennas in the Karoo either so the feed setup should be the least of their complaints.)

Anyway, our raw materials are 6 Measurement Sets at the relevant frequencies, and 6 x 2 x 2 FITS images describing the real and imaginary parts of the beam patterns (2) for the diagonal terms of the Jones matrix (2) for each of the (6) frequencies.

We'll also need a sky model, and for this simulation I've cooked up a LSM (beam_freq.lsm.html) that has six sources in it that steadily increase in radial distance from the phase centre in a pattern that vaguely resembles a spiral.

All of these products are attached below.